Intersection of Finite State Automata

Algorithm

Intersection can be defined in terms of complementation and union. Since we have algorithms to obtain the union and complement of a finite state automaton, we can give a construction to calculate their intersection.

Recall that the intersection of two sets S and T is equal to: (S^c U T^c)^c, where S^c is the complement of S.

The algorithm to calculate a finite state automaton which accepts the intersection of the languages accepted by two automatons A₁ and A₂ is thus the following:

1. Construct finite state automata B₁ and B₂ which accept the complement of the languages accepted by A₁ and A₂ (see the relevant algorithm).
2. Construct finite state automaton C which accepts the union of the languages accepted by B₁ and B₂ (see the relevant algorithm).
3. Remove useless and unreachable states from C, obtaining D (see the relevant algorithms to remove useless and unreachable states).
4. Minimise D to obtain E (see the relevant algorithm).
5. Calculate the inverse of E.

Note that steps 3 and 4 are not necessary, but are done to simplify step 5 (recall that to calculate the complement of a finite state automaton, the original automaton has to be made deterministic, which can be a very messy and error-prone process with large automata).

Example

Consider the following two FSA:

1. Start by constructing automata which recognise the complement of these automata:

   

2. Take the union of these resultant automata:

   

3. Remove useless and unreachable states:

   

4. Minimise automaton:

   

5. Construct an automaton accepting the complement of the language recognised by the minimised automaton:

   

Exercises

Calculate an automaton which recognises the intersection of the languages recognised by the following two automata:
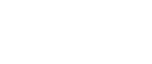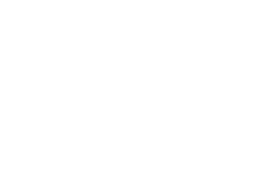